Lasso Regression

Lasso Regression is an example of regularization method.

Here, we will only talk about lasso regression. As I have mentioned earlier, lasso regression is an example of regularization method which develop model on larger number of features, where large number of features either means one of the below mentioned points:

1. The dataset is large enough to make the model overfit. Minimum of 10 features can do so.

2. The dataset is large enough that causes the computational challenges. This situation arises where the dataset has millions and billions of features.

Lasso regression performs L1 regularization which means that a penalized term will be added whose value is equal to the absolute value of the magnitude of the coefficient.

Lasso regression helps to reduce the overfitting and it is particularly useful for feature selection and when you have several independent variables that are useless. It will consider only those features

Lasso regression can be very useful if we have several independent variables that are useless.

Lasso Regression: Min (sum of the squared residuals + alpha * |slope|)

Lasso regression is similar to ridge regression. It works by introducing a bias term but instead of squaring the slope, the absolute value of slope is added as a penalized term.

Ridge Regression

Min(sum of the squared residuals +𝞪 * slope2 )

Lasso Regression

Min(sum of squared residuals + 𝞪 * |slope|)

Let’s take an example, suppose we have a dataset having salary of employees in one column and in the other column we have years of experience and we need to develop a model in which by giving years of experience as input, the model will predict the salary for the employee.

Years of Experience	Salary
1.6	4,00,000
3.2	5,00,000
1	2,50,000
5.7	7,00,000

Now splitting the data using “sklear” library, the code will look something like this.

from sklearn.model_selection impor train_test_split
X_Train, X_Test, Y_Train, Y_Test = train_test_split(x, y, test_size = 1/3, random_state = 0)

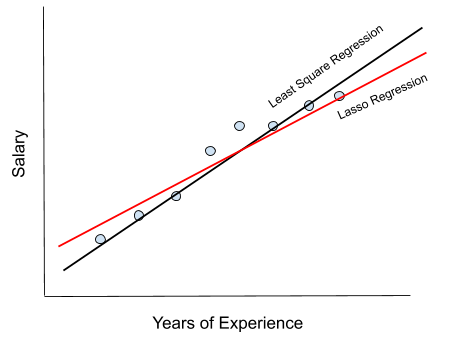
After splitting the data, we need to plot the data and the line of best fit is obtained and it will look something like this. The sum of squared residuals is zero for the training dataset. Min(sum of the squared residuals +𝞪 * slope2 )

However, for the testing data, the sum of squared residuals is not zero and it is having high variance. Variance Means That There Is A Difference In Fit (Or Variability) Between The Training Dataset And The Testing Dataset.

Lasso regression works by improving the variance and in return the slope will change depending upon the situation.

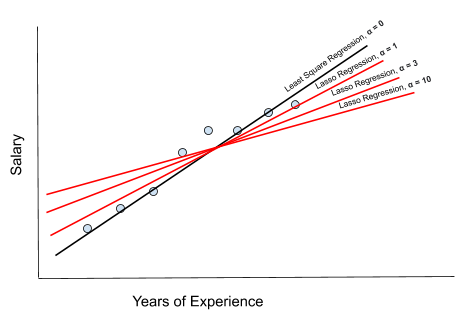
Effect of 𝜶 on Lasso Regression:

As alpha increases, the slope of the regression line is reduced and becomes more horizontal.

As alpha increases, the model becomes less sensitive to the variations of the independent variable (years of experience).

When to use Lasso Regression!

Lasso regression is basically used as an alternative to the classic least square to avoid those problems which arises when we have a large dataset having a number of independent variables (features).

Limitations of Lasso Regressions

Lasso Regression gets into trouble when the number of predictors are more than the number of observations. Lasso Regression will take most of the predictors as non-zero, irrespective of the fact that even all the predictors may be relevant.
The other limitation is that if there are two or more highly collinear variables then Lasso Regression will select one of them randomly which is not a good technique in data interpretation. With all being said, we have come to the end of this article. I hope that you get a gist of what Lasso regression really is. Try to implement it in your previous machine learning model and see how it improves the model’s performance.

Article By : ADIL HUSSAIN

If you are Interested In Machine Learning You Can Check Machine Learning Internship Program

Also Check Other technical and Non Technical Internship Programs